Unlocking Unlimited Data
"Do not underestimate the seductive power of math." - Rachel Hartman
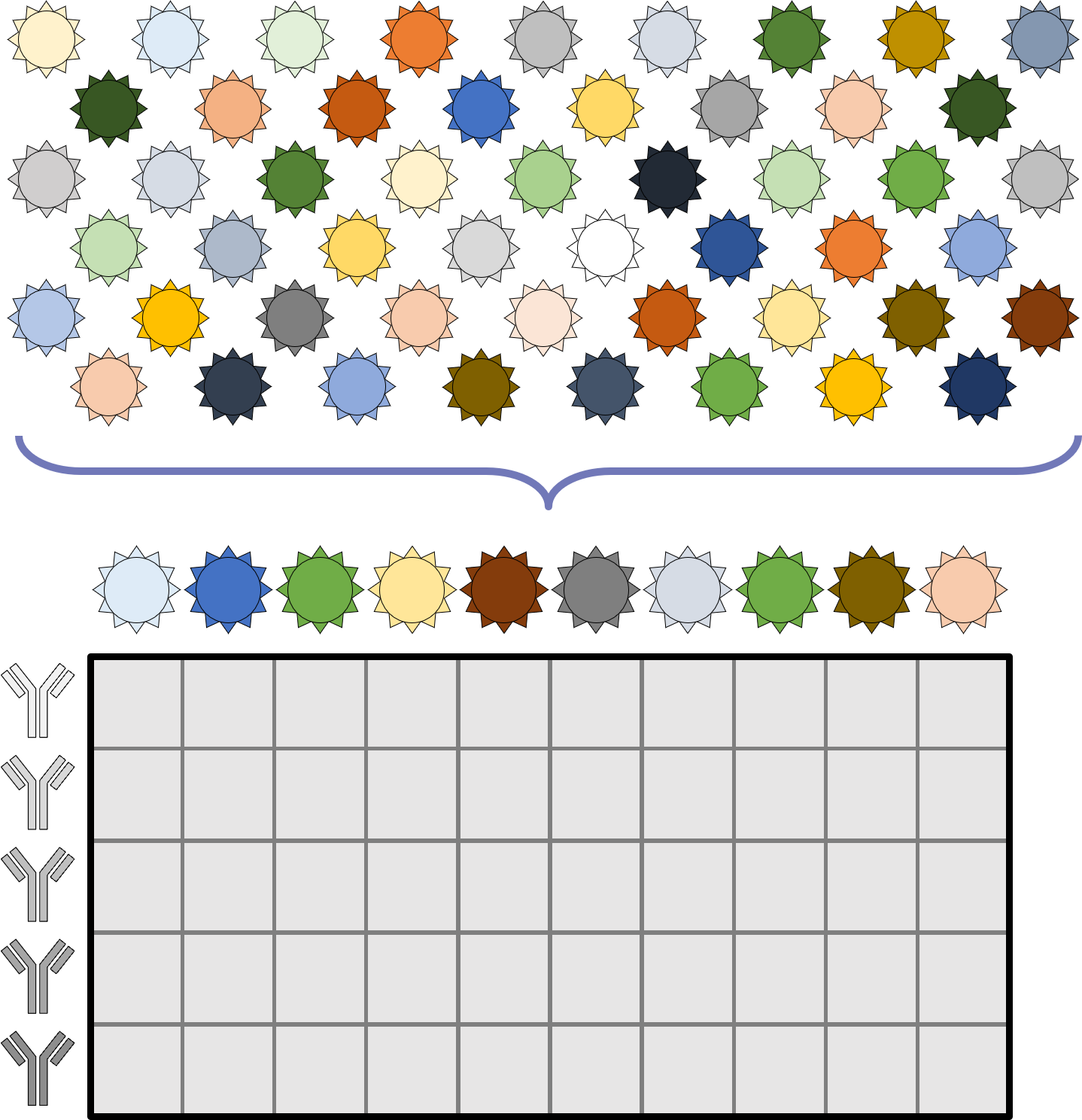
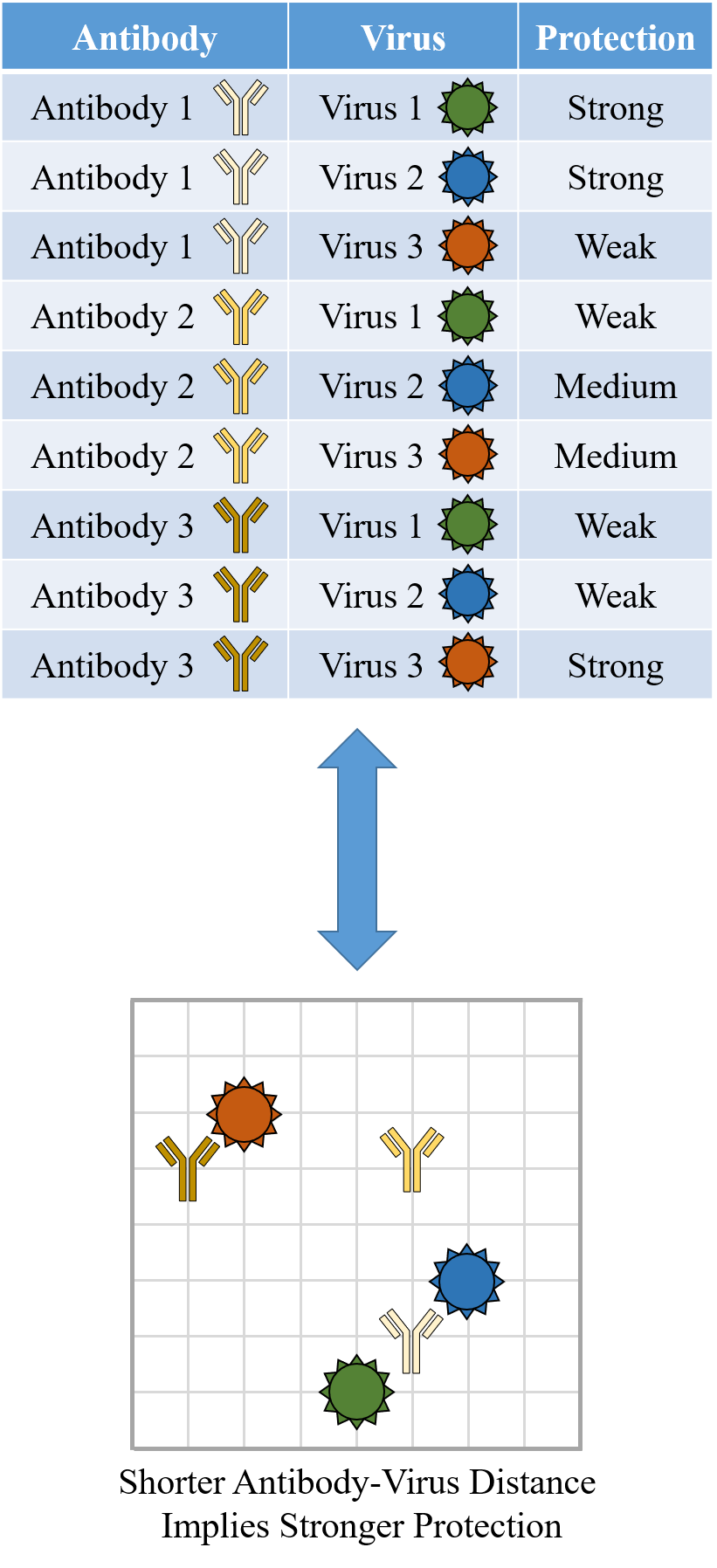
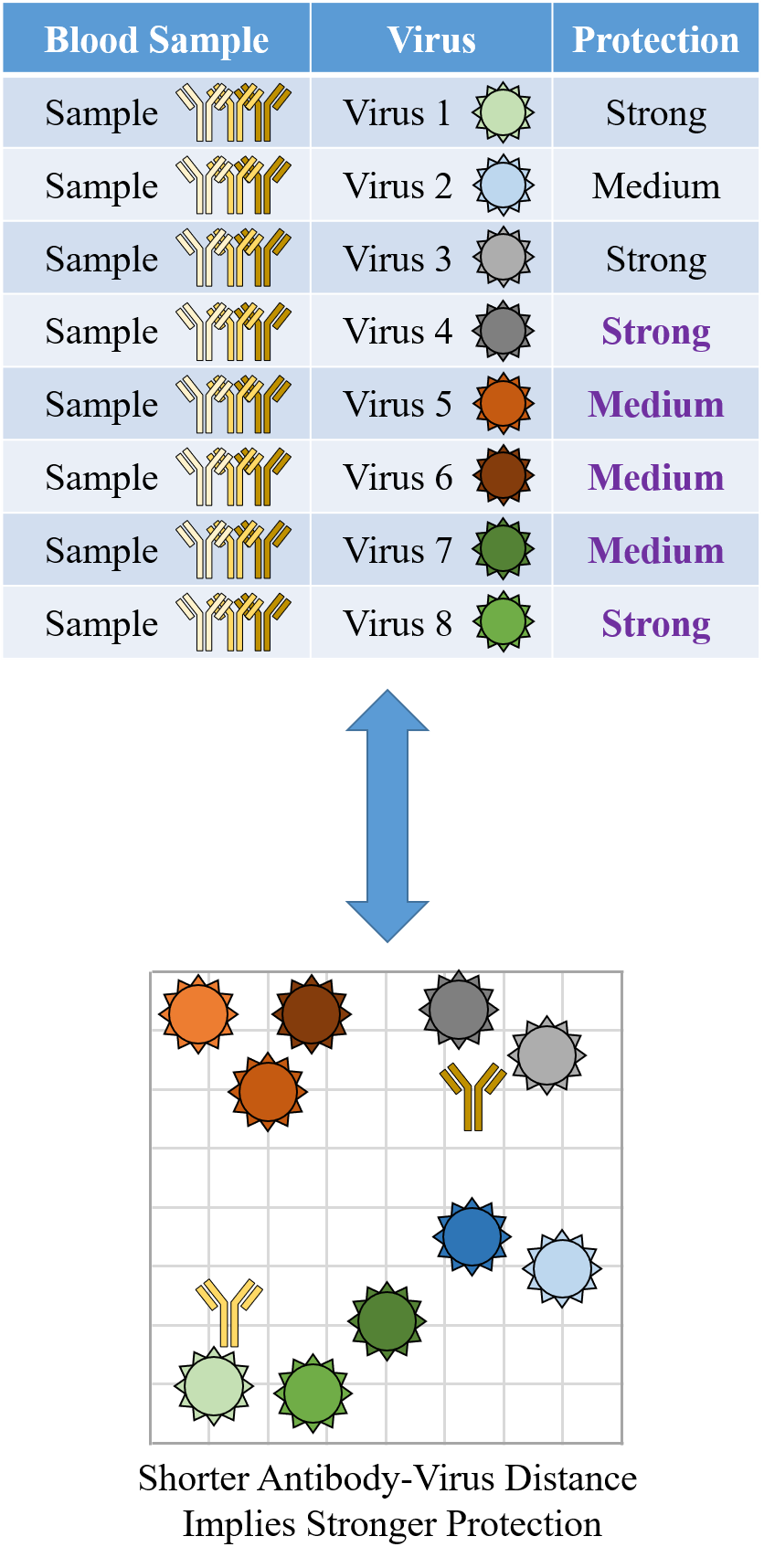
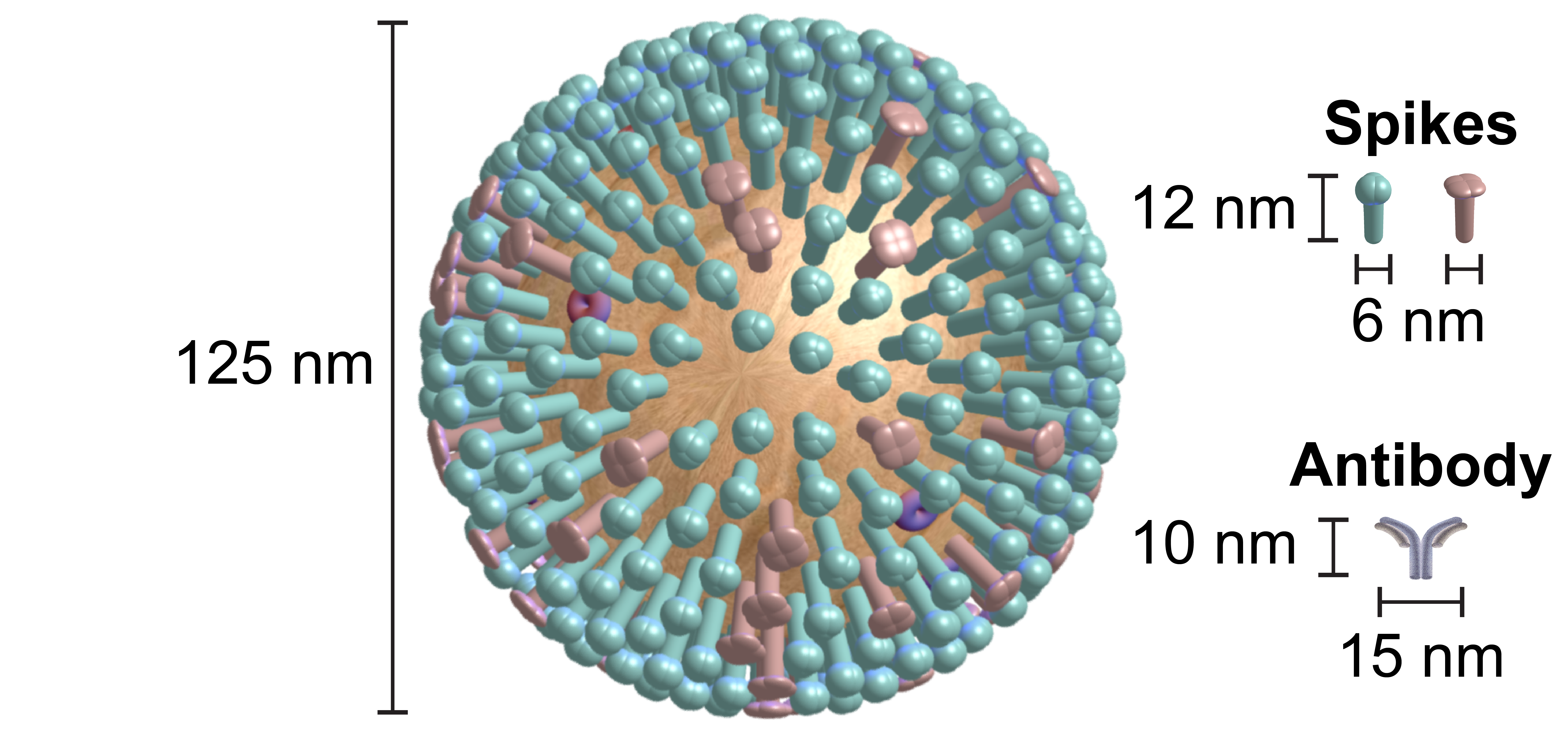
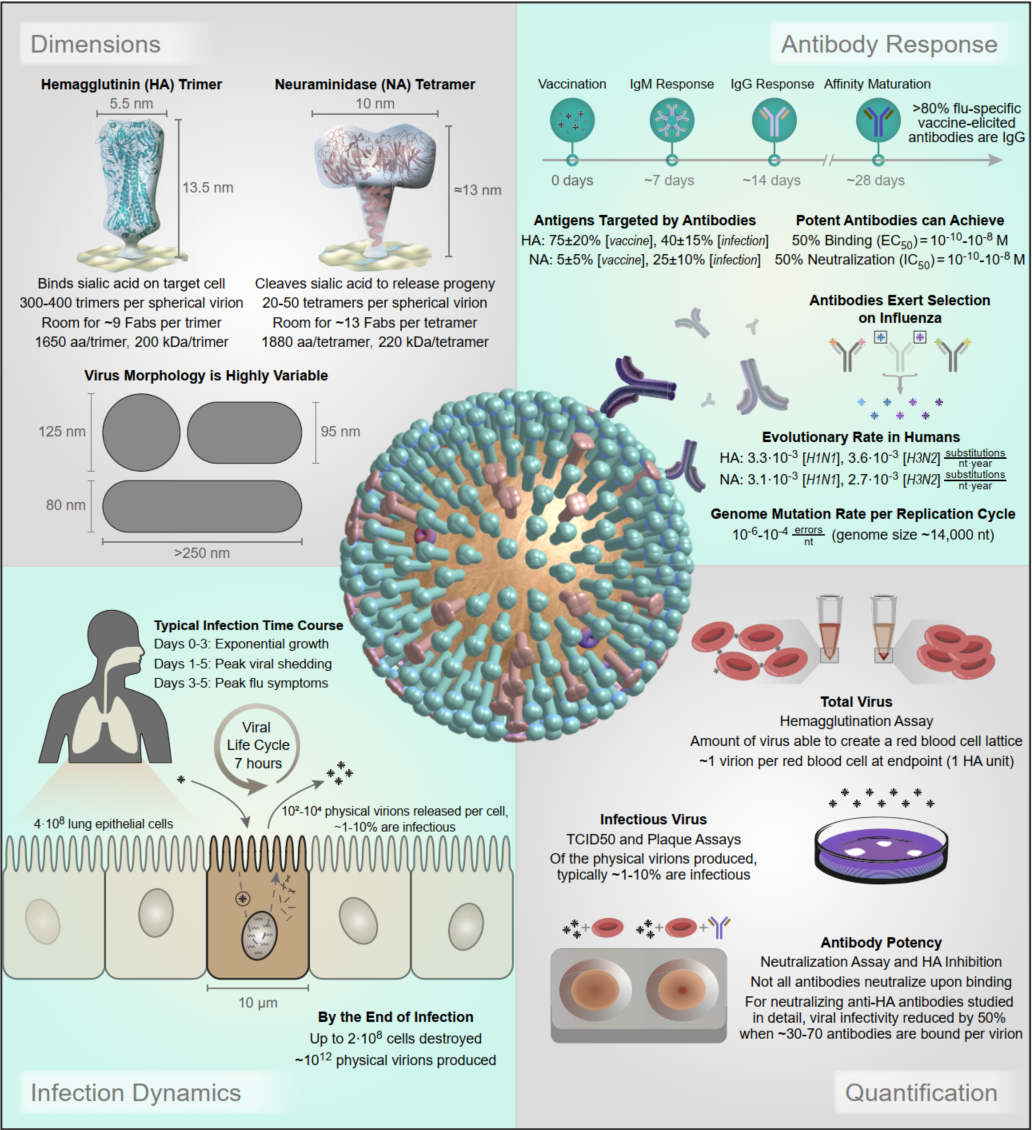
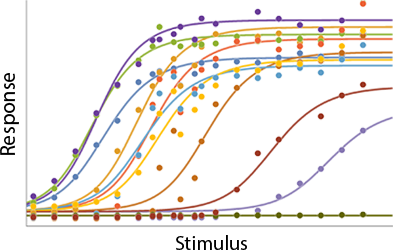
A central goal of immunology research is to elicit a potent antibody response that inhibits as many viruses as possible, ideally leaving a virus with no opportunities to mutate and escape. Experiments often measure how antibodies inhibit dozens of different viruses.
Unfortunately, this constitutes a tiny fraction of all possible viruses - each year hundreds of new variants emerge and join the worldwide melee. When researchers seek antibodies that comprehensively inhibit the whole gamut of viruses, they often choose variants that have little-to-no overlap with other studies. This makes it difficult to compare antibody responses across studies, and each dataset ends up being analyzed in isolation.
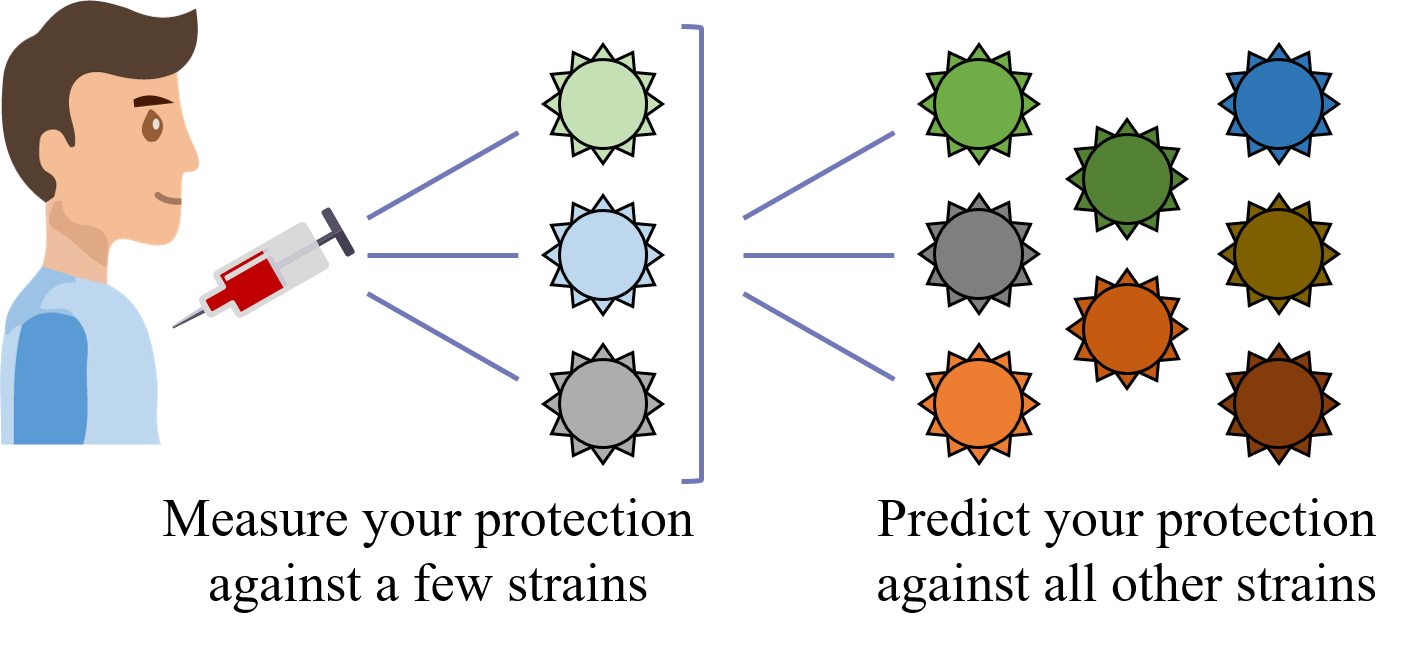
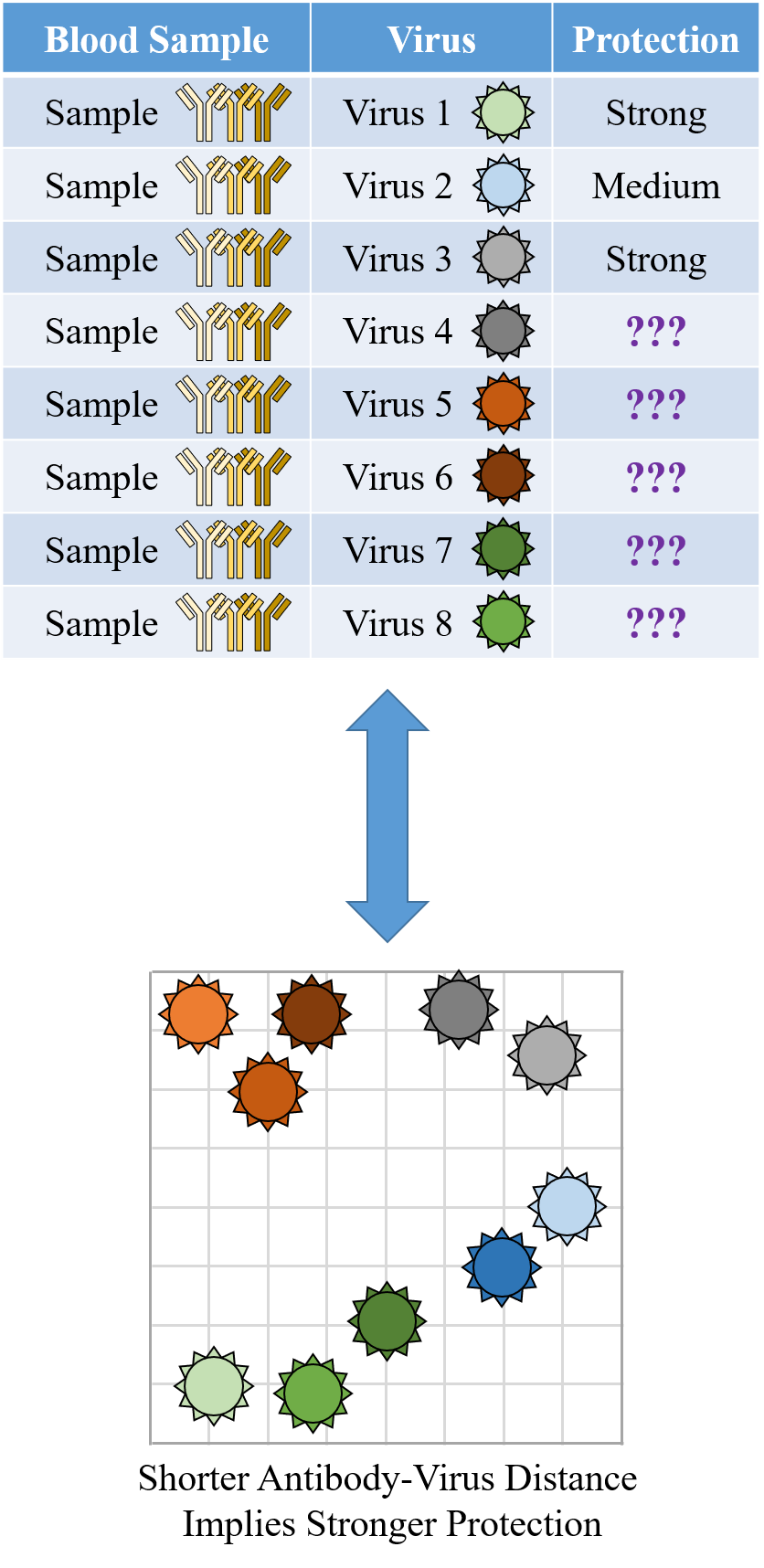
What we need is a framework that learns the underlying patterns in the data and extrapolates how every antibody would inhibit each virus. Is this possible...?
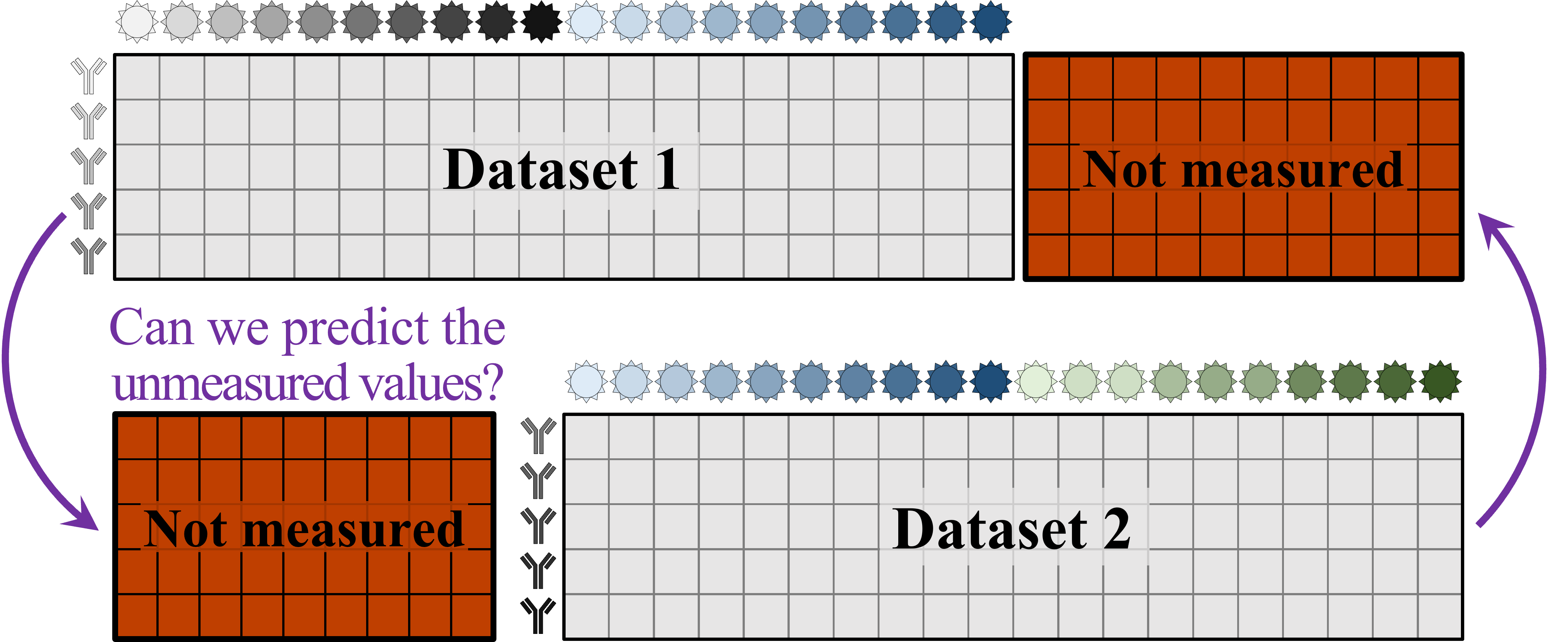
Indeed it is! By combining data, we can predict how the antibodies in one dataset would inhibit the viruses from any other dataset. With this mindset, the different virus panels in each study are not a weakness, but rather an asset allowing us to better explore the space of possible viruses.
The implications are huge - each experiment takes significant time and resources, and by combining datasets we can massively expand the number of measurements, often by more than 10x, without any additional work!
Of course, things are not that easy. Biology is riddled with anecdotes highlighting how tiny differences in a protocol can lead to dramatically different results. Even without such errors, there is immense diversity among antibodies, so the patterns of virus inhibition seen in one dataset may not be reflected in another dataset.
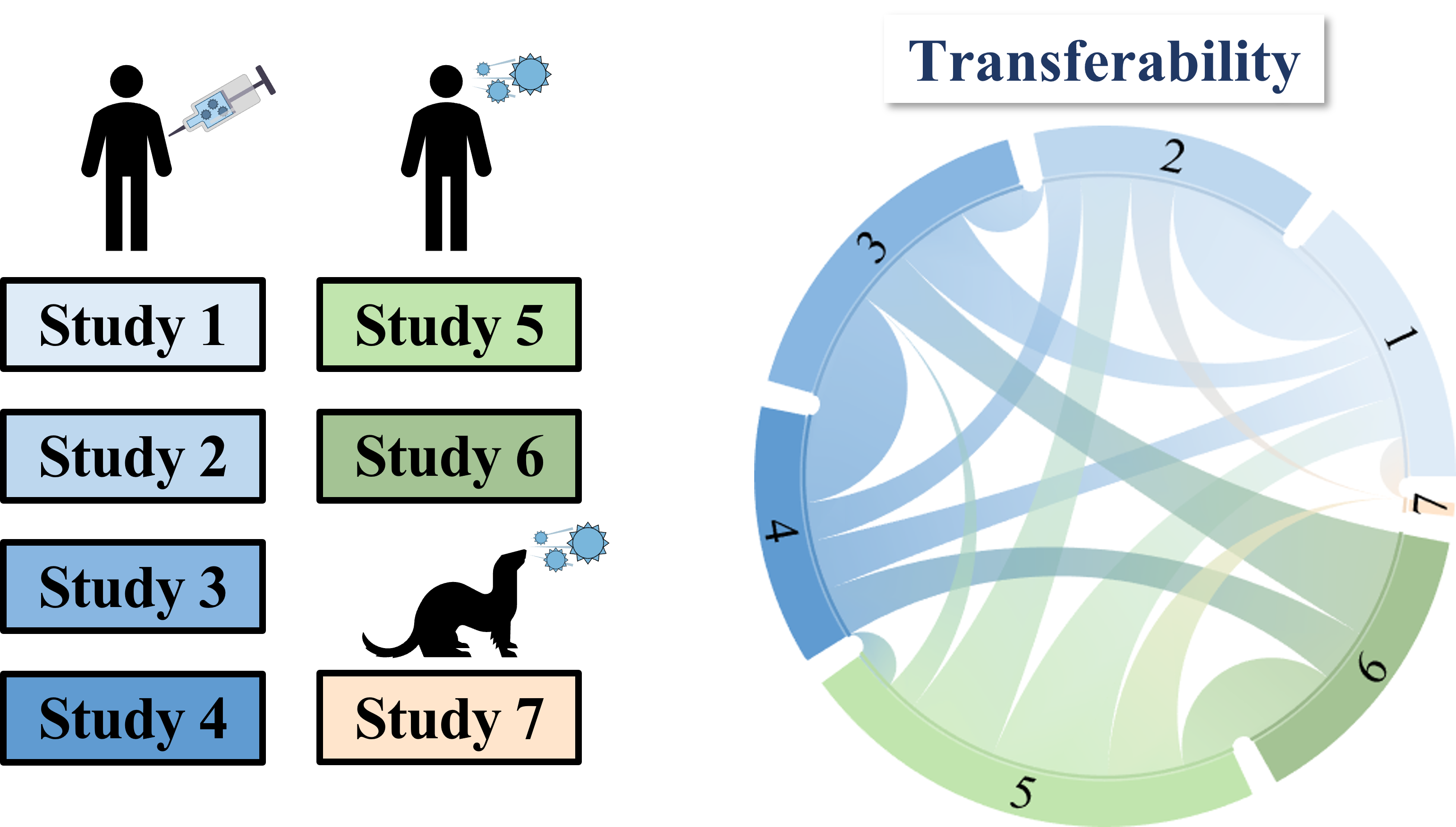
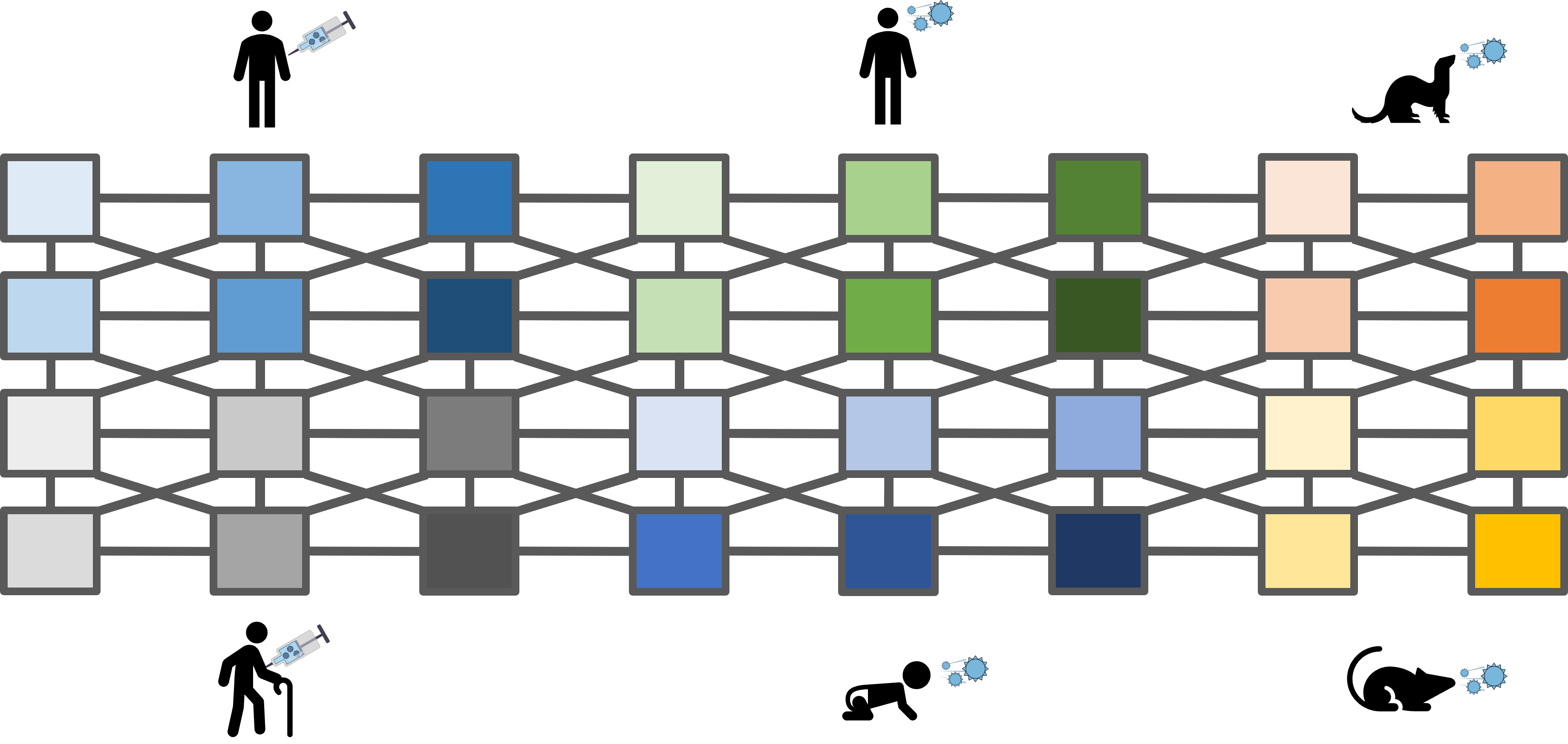
To overcome this difficulty, we develop a machine learning algorithm to quantify the transferability of information between two datasets. In other words, how does the behavior of viruses in one study inform the behavior of viruses in another study? We display the transferability using a chord diagram, which is visually striking but a bit tricky to interpret the first time you see it. So let's look at one specific study...
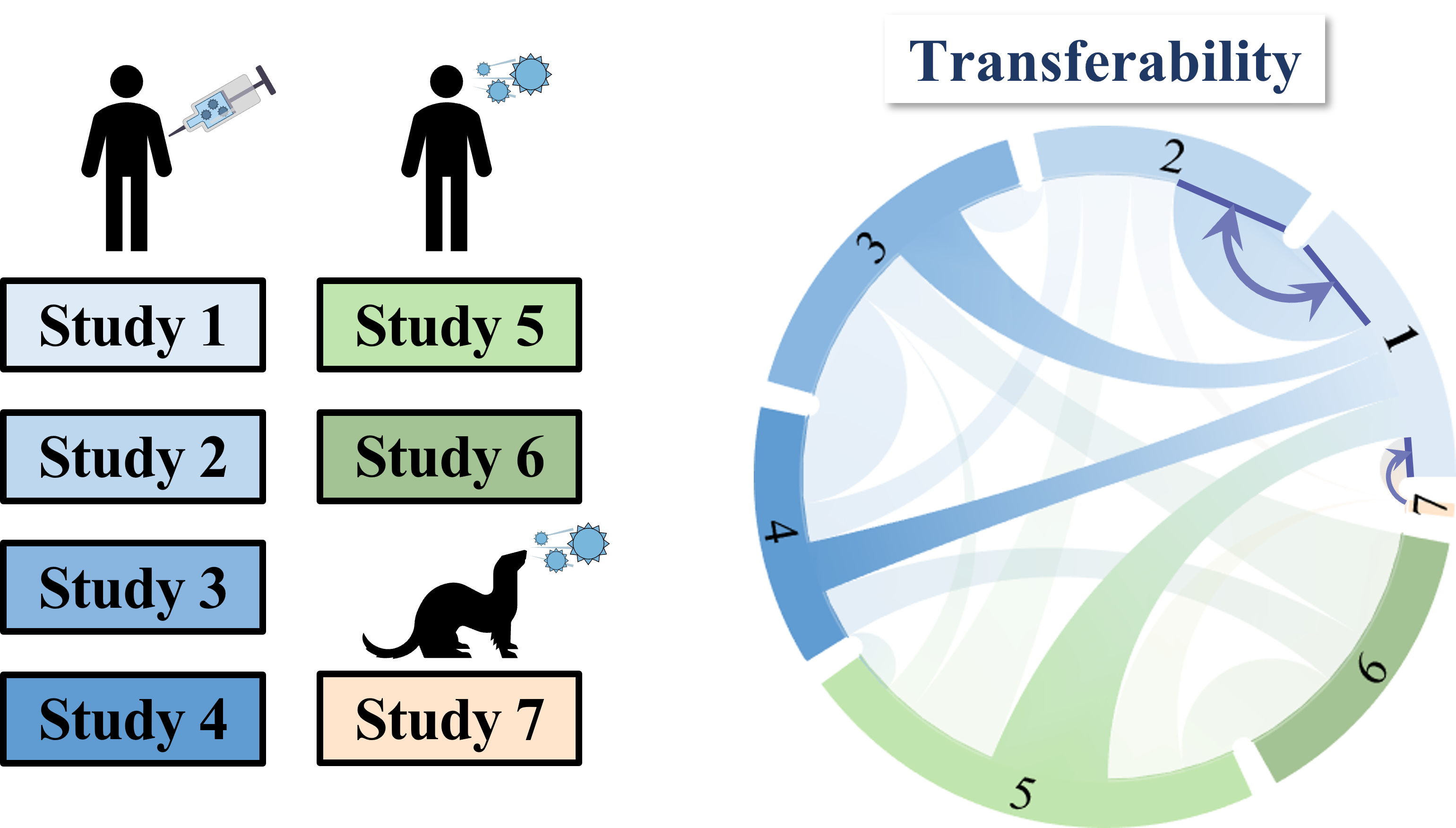
Each band in the diagram represents a double-sided arrow, where a thicker band implies greater transferability. Study 1 is highly informative of Study 2 (and vice versa), whereas Study 1 and 3 are less informative of one another. Ferrets (shown in Study 7) turn out to be very different from humans, and we need to understand these relationships more deeply, since influenza surveillance is conducted using ferrets.
One surprising result was that human vaccination studies (shown in blue) and human infection studies (green) can have high transferability, even though the participants in the infection studies had never received an influenza vaccine in their life! By quantifying the transferability between datasets, we can determine which factors (such as age or infection history) give rise to distinct antibody responses, and which factors don't matter.
Of course, this is just the beginning. The power of this approach is that as we add more datasets, they are expanded by previous studies, but they also expand those studies in return. Thus, we grow a network that embodies the full extent of our knowledge on antibody-virus interactions.
This data-driven approach can be readily expanded to other viruses, or more generally to other low-dimensional datasets. I predict that the main limitation of these methods will be in how creatively we will apply them. If you have any ideas, or are simply excited by this approach, feel free to contact me and I would be happy to discuss this "mathematical superpower." You can also read our manuscript for more details.